I liked this problem. It's straightforward enough to be an Easy but leaves room for a clean, single-pass, in-place solution. I dislike the hints since they promote an inelegant implementation, but linear is linear, and time complexity is the main metric LeetCode tests.
Copied!1class Solution: 2 def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]: 3 length = len(nums) 4 stop = -1 5 j = 0 6 for i in range(-k, length): 7 if i + k < length and nums[i + k] == key: 8 stop = i + (k << 1) 9 if i >= 0 and i <= stop: 10 nums[j] = i 11 j += 1 12 del nums[j:] 13 return nums
I considered making stop an exclusive index initialized to 0 (negative initializations are ugly), but that would have required an extra + 1 on line 8.
Now is NOT a good time for a Hard. I already spent all night on this blog.
😔
Anyways, the problem seemed doable at first. Heck, I understood the assignment in just a few minutes. Record time!
Then I realized numbers could be negative. Yikes.
Yikes.
That was bad. And not the good kind of bad that tickles your brain until you find an elegant, linear-time solution. I was hoping I could pick the next smallest product at every step.
Copied!1# Results of incrementing each idx 2cand = [ 3 nums1[idx[0] + 1] * nums2[idx[1]] if idx[0] + 1 < lim[0] else MAX, 4 nums1[idx[0]] * nums2[idx[1] + 1] if idx[1] + 1 < lim[1] else MAX, 5 nums1[idx[2] + 1] * nums2[idx[3]] if idx[2] + 1 < lim[2] else MAX, 6 nums1[idx[2]] * nums2[idx[3] + 1] if idx[3] + 1 < lim[3] else MAX, 7]
It was a binary search. I hate binary searches.
They show up in the most random places, no matter the size of the search space. Verifying a condition from -10¹⁰ to 10¹⁰ is practically brute force.
I suspected the solution would be a binary search on the output value, but I started with other approaches in hopes of something nicer. No dice, but at least sign tracking proved relevant, and my sign_cutoff function was transferable.
Unfortunately, the verification function contained edge cases galore. I guess that should be expected of a Hard. But you know it's bad when I pull out the local editor.
Copied!1class Solution: 2 def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int: 3 len1 = len(nums1) 4 len2 = len(nums2) 5 6 def sign_cutoff(nums): 7 # Returns index of first nonnegative number 8 left, right = 0, len(nums) - 1 9 while left < right: 10 mid = (left + right) // 2 11 if nums[mid] < 0: 12 left = mid + 1 13 else: 14 right = mid 15 16 if nums[left] >= 0: 17 return left 18 return len(nums) 19 20 sc1 = sign_cutoff(nums1) 21 sc2 = sign_cutoff(nums2) 22 i = sc1 23 while i < len1 and nums1[i] == 0: 24 i += 1 25 z1 = i - sc1 # number of zeros 26 j = sc2 27 while j < len2 and nums2[j] == 0: 28 j += 1 29 z2 = j - sc2 # number of zeros 30 nzero = z1 * len2 + z2 * len1 - z1 * z2 31 nneg = sc1 * (len2 - sc2 - z2) + sc2 * (len1 - sc1 - z1) 32 33 print(f'{sc1=} {z1=} {sc2=} {z2=} {nneg=} {nzero=}') 34 35 def prods_leq(limit): 36 # Returns the number of products less than or equal to limit 37 if limit == 0: 38 return nneg + nzero 39 40 if limit > 0: 41 nless = nneg + nzero 42 # i < 0, j < 0 43 j = 0 44 for i in range(sc1 - 1, -1, -1): 45 while j < sc2 and nums1[i] * nums2[j] > limit: 46 j += 1 47 nless += sc2 - j 48 # i > 0, j > 0 49 j = len2 - 1 50 for i in range(sc1 + z1, len1): 51 while j >= sc2 + z2 and nums1[i] * nums2[j] > limit: 52 j -= 1 53 nless += j - (sc2 + z2) + 1 54 return nless 55 56 nless = 0 57 # i < 0, j > 0 58 j = sc2 + z2 59 for i in range(sc1): 60 while j < len2 and nums1[i] * nums2[j] > limit: 61 j += 1 62 nless += len2 - j 63 # i > 0, j < 0 64 j = 0 65 for i in range(sc1 + z1, len1): 66 while j < sc2 and nums1[i] * nums2[j] <= limit: 67 j += 1 68 nless += j 69 return nless 70 71 left, right = -10 ** 10, 10 ** 10 72 while left < right: 73 mid = (left + right) // 2 74 if prods_leq(mid) >= k: 75 right = mid 76 else: 77 left = mid + 1 78 return left
Certainly not my best code. Most logic occurs in prods_leq. There's probably some symmetry there that I screwed up. I encountered so many off-by-one errors that by the end, I had accumulated 7/8 testcases.
Maybe f*#! around and find out was not the right approach.
The editorial solution is much shorter but has worse time complexity. It uses a binary search to determine the j corresponding to each i.
I considered adding early-out conditions and merging some cases, but I'm too tired at this point.
This problem was a relief after yesterday's... event. I'd place it on the easier end of Medium problems. Two edge cases threw me for a loop (the two if statements below), but solving otherwise went smoothly.
Copied!1class Solution: 2 def longestSubsequence(self, s: str, k: int) -> int: 3 length = len(s) 4 k = bin(k)[2:] 5 out = len(k) 6 if out > length: 7 return length 8 if s[length - out:] > k: 9 out -= 1 10 out += s[:length - out].count('0') 11 return out
I initially used string indexing but later refactored to slicing. I'll trade memory for elegance any day.
Copied!1int longestSubsequence(char* s, int k) { 2 int out = 32 - __builtin_clz(k); 3 int length = strlen(s); 4 if (out > length) { 5 return length; 6 } 7 char* endptr; 8 if (strtol(s + length - out, &endptr, 2) > k) { 9 out--; 10 } 11 int stop = length - out; 12 for (int i = 0; i < stop; i++) { 13 if (s[i] == '0') { 14 out++; 15 } 16 } 17 return out; 18}
To feel better about Python's gratuitous copying of string slices, I ported my logic to C.
This Hard caught me a little off guard. We had one two days ago. I was expecting a Medium.
Anyways, I loved this problem! It made me feel so, so clever. After racking my brain for days on end, I happened upon my greatest insight...
* drumroll *
reading the f**king constraints.
In particular, the constraint that n < k * 8. I hope sarcasm has conveyed my utter disappointment. They got my hopes up with the topics list. I love Greedy problems.
Luckily, prior analysis had tempered my expectations. I had already considered the situation where s = abccaccb and k = 2. The subsequence ab works but is not necessarily a prefix of the longest subsequence. Even now, I'm not entirely sure why Greedy was on there.
Back to the insight. Here are some comments I made:
Copied!1# n is at most 8 * k 2# ss is at most 8 characters 3# 256 * length time complexity 4# linear!
I also made the faulty assumption that the longest subsequence would be contained within the first n // k characters, but regardless, I discovered that the solution would be brute force. Hooray!
The assumption actually worked quite well. With n // k changed to ceil(n / k), my program passed 304 / 313 testcases. Note that n here is the number of characters in s occurring at least k times. With the subsequence search space expanded to the first 2 * n // k characters, my program passed 312 / 313 testcases.
At this point, any sane person would just hardcode the 313th test.
I decided to be a sane person. Don't tell LeetCode.
Runtime beat 46.34%. Memory beat 36.59%. Blending right in!
Anyways, the assumption proved faulty because the first occurrence of a subsequence can extend deep into s while remaining occurrences bunch up at the end. Use of the proper search space led to Time Limit Exceeded.
I took a short break from the problem, but the various loopholes didn't sit right with me, so I eventually went back to the drawing board. Sorry to disappoint.
I promise I have a life.
I promise I have a life.
I do not promise I have a sleep schedule.
Luckily, most of my code was reusable, and I thought of switching to a character bank relatively quickly.
Copied!1class Solution: 2 def longestSubsequenceRepeatedK(self, s: str, k: int) -> str: 3 # Only care about characters that appear at least k times 4 cnt = Counter(s) 5 new_s = '' 6 for c in s: 7 if cnt[c] >= k: 8 new_s += c 9 s = new_s 10 length = len(s) 11 12 def is_valid(ss): 13 # Determines if ss occurs k times in s 14 idx, completed = 0, 0 15 sslen = len(ss) 16 remaining = sslen * k 17 for i, c in enumerate(s): 18 if c == ss[idx]: 19 idx += 1 20 remaining -= 1 21 if idx == sslen: 22 idx = 0 23 completed += 1 24 if completed == k: 25 return True 26 if remaining >= length - i: 27 return False 28 return completed == k 29 30 ssbank = {char: n // k for char, n in cnt.items()} 31 maxlen = length // k 32 valid = [] 33 34 def dfs(ss, bestlen): 35 if len(ss) == maxlen: 36 return bestlen 37 for c in ssbank: 38 if ssbank[c]: 39 ssbank[c] -= 1 40 ss += c 41 if is_valid(ss): 42 if len(ss) >= bestlen: 43 valid.append(ss) 44 bestlen = len(ss) 45 bestlen = dfs(ss, bestlen) 46 ss = ss[:-1] 47 ssbank[c] += 1 48 return bestlen 49 50 bestlen = dfs('', 0) 51 52 if valid: 53 return max(filter(lambda ss: len(ss) >= bestlen, valid)) 54 55 return ''
The program uses a depth-first search to construct and validate subsequences. If a subsequence fails, I kill off its bloodline.
There's probably a technical term for that, but violence is more fun.
The editorial solution is actually quite elegant. Turns out my is_valid was much more verbose than necessary. Swapping it for the editorial one-liner brought my runtime from 52.03% to 95.12%. Yay generators. The editorial also opts for a nice, queue-based breadth-first search. I'll paste it below for those too lazy to find it.
Copied!1class Solution: 2 def longestSubsequenceRepeatedK(self, s: str, k: int) -> str: 3 ans = "" 4 candidate = sorted( 5 [c for c, w in Counter(s).items() if w >= k], reverse=True 6 ) 7 q = deque(candidate) 8 while q: 9 curr = q.popleft() 10 if len(curr) > len(ans): 11 ans = curr 12 # generate the next candidate string 13 for ch in candidate: 14 nxt = curr + ch 15 it = iter(s) 16 if all(ch in it for ch in nxt * k): 17 q.append(nxt) 18 return ans
I am now ashamed of my line count.
In the end, I didn't find this problem that bad. The big insight was still exciting given my prior state, head.empty. I certainly enjoyed this problem more than Wednesday's, though Wednesday was a very low bar.
Nevertheless, problems governed by testcase constraints feel a little pointless. Though real-world problems can (and often do) have constraints, succumbing to brute force because it *passes the tests* is boring and bound to disappoint.
Finally an Easy. This problem was alright, though with Python 3, it mostly just tests how well you know your builtins. I brainstormed some very ugly ideas to deal with repeats (one involved a Counter), but luckily, those never saw the light of day. I wrote two solutions: one that just sorts and one that uses a heap.
Copied!1class Solution: 2 def maxSubsequence(self, nums: List[int], k: int) -> List[int]: 3 top = sorted([(n, i) for i, n in enumerate(nums)])[-k:] 4 top.sort(key=lambda ni: ni[1]) 5 return [ni[0] for ni in top]
Heap syntax is so cursed in Python 3. And there's no max heap. At least this problem didn't require one.
Copied!1class Solution: 2 def maxSubsequence(self, nums: List[int], k: int) -> List[int]: 3 top = [] 4 heapify(top) 5 for i, n in enumerate(nums): 6 if i < k: 7 heappush(top, (n, i)) 8 else: 9 heappushpop(top, (n, i)) 10 top.sort(key=lambda ni: ni[1]) 11 return [ni[0] for ni in top]
Have a Rust solution too!
Copied!1impl Solution { 2 pub fn max_subsequence(nums: Vec<i32>, k: i32) -> Vec<i32> { 3 let length = nums.len(); 4 let mut sorted = nums.into_iter().enumerate().collect::<Vec<(_, _)>>(); 5 sorted.sort_by_key(|it| it.1); 6 let top = &mut sorted[length - k as usize..length]; 7 top.sort_unstable(); 8 top.into_iter().map(|it| it.1).collect() 9 } 10}
The Rust implementation was meant to take ten minutes. Unfortunately, I forgot that Rust syntax isn't nearly as straightforward as Python syntax. Remind me to use an actual editor next time I'm feeling masochistic.
Also, I love functional programming in Rust, but sorting ruins everything.
This problem was good but pretty hard for me. Although I found the approach almost immediately, I struggled with implementation. I couldn't decide whether to make i and j inclusive or exclusive and whether to start them at the center or edges. At one point, there was even a k. And naturally, I had several off-by-one errors.
LeetCode problems have ingrained in me a phobia of repeated numbers, so I also spent a while considering how my program would respond to them. My apprehension led to various while loops and lots of pain. I got rid of them after debugging the default tests though.
Copied!1while i + 1 < length and nums[i] == nums[i + 1]: 2 i += 1
For a while, my program was passing testcases 1-19 but failing on the 20th. Intermediate failures almost always result from Time Limit Exceeded or edge cases, so when nothing about the test jumped out at me, I figured the bug must be related to repeated numbers.
Copied!1[14,4,6,6,20,8,5,6,8,12,6,10,14,9,17,16,9,7,14,11,14,15,13,11,10,18,13,17,17,14,17,7,9,5,10,13,8,5,18,20,7,5,5,15,19,14] 222
With repeats removed, the test passed. Ergo repeats were the problem.
I thought.
Well anyways, I proceeded to pull out my iPad (whoa) to painstakingly review my logic. This bug was particularly difficult to catch because the modulo system prevented me from knowing whether my program was undercounting or overcounting.
Undercounting or overcounting. Wanna take a guess?
3... 2... 1...
Neither.
But Alex! How could that possibly be???
Because I'm stupid. That's how. Brain? We don't do that here.
Copied!1class Solution: 2 def numSubseq(self, nums: List[int], target: int) -> int: 3 MOD = 10 ** 9 + 7 4 length = len(nums) 5 nums.sort() 6 j = bisect_right(nums, target // 2) 7 i = j - 1 8 delta = 1 9 out = 0 10 while i >= 0: 11 while j < length and nums[i] + nums[j] <= target: 12 delta = delta * 2 % MOD 13 j += 1 14 out = (out + delta) % MOD 15 i -= 1 16 delta = delta * 2 % MOD 17 return out
Guess what! If the problem specifies that your answer should be taken modulo 10⁹ + 7, then your answer should probably be less than 10⁹ + 7.
So anyways, it took over half an hour to realize that line 14 needed a MOD as well. The testcase output highlighted that most of my digits were matching, but at the time, I explained it away as pure coincidence.
> Expected: 272187084
Repeated numbers ultimately required no special treatment, but hey, delusion and suffering are essential components of the LeetCode grind.
This problem was pretty straightforward. My original plan was to sort nums and make some state variables, but then I realized a Counter implementation would probably be easier.
Copied!1class Solution: 2 def findLHS(self, nums: List[int]) -> int: 3 cnt = Counter(nums) 4 return max(cl + (cnt[nl + 1] if nl + 1 in cnt else -cl) for nl, cl in cnt.items())
My submission scored 65.29% on runtime. Ewww. Disowned.
Copied!1class Solution: 2 def findLHS(self, nums: List[int]) -> int: 3 nums.sort() 4 num_prev, cnt_prev = nums[0], 0 5 num_curr, cnt_curr = nums[0], 0 6 best = 0 7 for num in nums: 8 if num == num_curr: 9 cnt_curr += 1 10 continue 11 if num_curr == num_prev + 1 and cnt_curr + cnt_prev > best: 12 best = cnt_curr + cnt_prev 13 num_prev, cnt_prev = num_curr, cnt_curr 14 num_curr, cnt_curr = num, 1 15 if num_curr == num_prev + 1 and cnt_curr + cnt_prev > best: 16 best = cnt_curr + cnt_prev 17 return best
This fella scored 96.80%. Hooray!
But then I reran the program and received a lukewarm 56.05%. Three times over.
I also copied several top submissions and ran them myself. They scored pretty average. Moral of the story? Always take LeetCode percentiles with a grain of salt, especially on Easy problems.
Alternatively, claim really really confidently that you are the best, and your dreams just might come true.
Copied!1# Nothing to see here 2__import__('atexit').register(lambda: open('display_runtime.txt', 'w').write('0'))
This problem was probably the easiest so far. I brainstormed the solution immediately. The only edit I had to make was adding 1 for the case where Alice doesn't make a typo.
On a side note, it was fun for the problem to have a premise. I wonder why Alice is typing abbcccc though.
Copied!1class Solution: 2 def possibleStringCount(self, word: str) -> int: 3 return 1 + sum(word[i] == word[i + 1] for i in range(len(word) - 1))
Copied!1class Solution: 2 def possibleStringCount(self, word: str) -> int: 3 it = iter(word) 4 next(it) 5 return 1 + sum(f == l for f, l in zip(it, iter(word)))
Copied!1class Solution: 2 def possibleStringCount(self, word: str) -> int: 3 out = 1 4 for i in range(len(word) - 1): 5 if word[i] == word[i + 1]: 6 out += 1 7 return out
Copied!1class Solution: 2 def possibleStringCount(self, word: str) -> int: 3 prev = None 4 out = 1 5 for c in word: 6 if c == prev: 7 out += 1 8 prev = c 9 return out
I tried four solutions in hopes of better runtime, though as we learned yesterday, runtime is a lie. I think it's a bit absurd that the sample below has the top performance.
Copied!1class Solution: 2 def possibleStringCount(self, word: str) -> int: 3 4 stack = [] 5 6 ans = 1 7 8 for w in word: 9 if not stack or (stack and w==stack[-1]): 10 stack.append(w) 11 else: 12 ans+=len(stack)-1 13 stack = [w] 14 15 #print(w,stack,ans) 16 17 ans+=len(stack)-1 18 19 20 21 22 return ans
Why the list bro.
Sit tight. I've got lots to talk about.
Of the Hard problems I've covered, this was probably my favorite. Not that there's been much competition. The other problems were all brute force. This problem actually required some thinking. Did I have a clue what was going on? Nope! But at least I had the opportunity to apply some logic and play with numbers.
Anyways, my first approach was a combinatorial solution. Something like stars and bars but with added restrictions. I spent a while pondering but gave up after reading the topics. Math was sadly absent. Some progress was transferable though, namely the logic to parse word into counts and the underlying goal of the problem. Some of my notes are below.
Copied!1# all single letters are fixed, we can ignore them 2# we now have sets of double or triple letters 3# and some limit length - k of how many we can delete 4# don't care about the actual letters - just maintain counts 5# require one from each set - just subtract 1 from each count
Line 3 was a dire mistake.
Copied!1# a1 + a2 + ... + an <= limit 2# 0 <= a1 <= l1, 0 <= a2 <= l2, ...
My second approach used memoization. I had seen Dynamic Programming under the topics but had no idea where to start and figured memoization would be easier. Implementation actually went quite smoothly. I had high hopes for a speedy completion.
Unfortunately, LeetCode is never that easy. I hit Time Limit Exceeded at 814/846 testcases. I'm not entirely sure why my code was failing. My best guesses are faulty memoization, too many stack frames, or the line 3 situation to be discussed shortly.
Regardless, I shifted gears to Dynamic Programming.
I think the switch would have been much smoother had I taken the time to fully understand my memoized approach. But I was impatient.
Most of my brainstorming revolved around a 2D array where rows corresponded to removal limits and column corresponded to cumulative groups of the counts array.
Copied!1# ways[lim][idx] is the number of ways to delete up to lim 2# characters from counts 0 to idx, inclusive 3# NVM DONT DO THIS 4 5# ways[lim][idx] is the number of ways to satisfy limit 6# using characters from counts 0 to idx, inclusive 7# where the amount we remove at idx is lim
Guess which approach I ultimately went with.
NVM DONT DO THIS
If you guessed wrong, you must be new here. Welcome! Nothing makes sense. Escape while you still can.
After bouncing between approaches, drawing some useless diagrams, rereading my memoized implementation, and I kid you not, looking for patterns between iterations in my print statement output, I finally got Dynamic Programming to work.
Now guess the result.
Good work! You're learning.
This result was actually surprising though. My approach felt efficient enough. It had approximately quadratic time complexity, specifically
where is the length of word. I wasn't even using the 2D array anymore, just two 1D arrays.
Wait a minute.
Is it time for another 𝓰𝓻𝓮𝓪𝓽𝓮𝓼𝓽 𝓲𝓷𝓼𝓲𝓰𝓱𝓽?
Well f*#!. I've been counting removals on the order of . To pass, I need to count inclusions on the order of . Because that's what LeetCode tests for.
Hey, let's start a list: the Laws of LeetCode.
- Runtime is fake.
- Read the damn constraints.
These laws of course only apply when convenient. If I score 100% on runtime, then runtime is a wonderful metric.
Back to the problem. I had to completely redo my implementation, counting the opposite quantity. Hooray for pain and suffering.
🫠
But then I realized: all my program needed was a little shift in mindset. I declared that my arrays would count inclusions, not removals. Nobody objected! Me, myself, and I were all in agreement.
Essentially, if you know (1) the number of ways to include less than limit characters and (2) the total number of combinations of characters, you can subtract to find the number of ways to include at least limit characters.
The total combinations of characters is just the product of all counts in the counts array, though the modulo system makes multiplying a little annoying. I wanted to use prod so badly. Alas, we must accomodate the poor children still working in C.
Luckily, I only had to modify 7 lines to get my implementation working, though the resultant hodgepodge was quite the eyesore.
Copied!1class Solution: 2 def possibleStringCount(self, word: str, k: int) -> int: 3 MOD = 10 ** 9 + 7 4 length = len(word) 5 if k >= length: 6 return 1 7 prev = None 8 count = 0 9 counts = [] 10 for c in word: 11 if c == prev: 12 count += 1 13 continue 14 if count > 1: 15 counts.append(count - 1) 16 prev = c 17 count = 1 18 if count > 1: 19 counts.append(count - 1) 20 limit = k - (length - sum(counts)) - 1 21 22 total = 1 23 for count in counts: 24 total = total * (count + 1) % MOD 25 26 if limit < 0: 27 return total 28 unique = len(counts) 29 30 prev = list(range(1, counts[0] + 1)) + [counts[0] + 1] * (limit + 1 - counts[0]) 31 32 for idx in range(1, unique): 33 curr = [0] * len(prev) 34 curr[0] = 1 35 for lim in range(1, limit + 1): 36 curr[lim] = curr[lim - 1] + prev[lim] 37 if lim > counts[idx]: 38 curr[lim] -= prev[lim - counts[idx] - 1] 39 curr[lim] %= MOD 40 prev = curr 41 42 return (total - prev[limit]) % MOD
It sure has personality!
Impressively, it scored 100.00% on runtime and 94.12% on memory. I challenged myself to clean up the implementation though. I managed to reduce the line count by 30%.
Copied!1class Solution: 2 def possibleStringCount(self, word: str, k: int) -> int: 3 MOD = 10 ** 9 + 7 4 if k >= len(word): 5 return 1 6 limit = k - len(word) 7 prev = None 8 count = 0 9 counts = [] 10 for c in word + '\0': 11 if c == prev: 12 count += 1 13 continue 14 if count > 1: 15 counts.append(count) 16 limit += count - 1 17 prev = c 18 count = 1 19 20 total = reduce(lambda tot, count: tot * count % MOD, counts) 21 if limit <= 0: 22 return total 23 24 ways = [1] * limit 25 for count in counts: 26 ways = list(accumulate(ways)) 27 for lim in reversed(range(count, limit)): 28 ways[lim] -= ways[lim - count] 29 30 return (total - ways[limit - 1]) % MOD
The refactored program has a runtime around 700 ms. For reference, my hodgepodge took around 1100 ms.
I also tested out numpy. Unfortunately, import statements tank the memory score, but the following program got down to 524 ms.
Copied!1from numpy import ones, cumsum, int32 2 3class Solution: 4 def possibleStringCount(self, word: str, k: int) -> int: 5 MOD = 10 ** 9 + 7 6 if k >= len(word): 7 return 1 8 limit = k - len(word) 9 prev = None 10 count = 0 11 counts = [] 12 for c in word + '\0': 13 if c == prev: 14 count += 1 15 continue 16 if count > 1: 17 counts.append(count) 18 limit += count - 1 19 prev = c 20 count = 1 21 22 total = reduce(lambda tot, count: tot * count % MOD, counts) 23 if limit <= 0: 24 return total 25 26 ways = ones(limit, dtype=int32) 27 for count in counts: 28 ways = cumsum(ways) % MOD 29 ways[count:] -= ways[:-count] 30 31 return (total - ways[limit - 1]) % MOD
I'm not entirely sure why the subtractions work, but they do, and that's all that really matters. It's 7 AM. I'm going to sleep.
It's the following afternoon. I decided to actually understand what my solution was doing. Just thought I would share my notes here.
I also rewrote the program in Rust. The operation took much longer than anticipated. The modulo requirement isn't so bad in Python because Python just takes care of overflow errors and the modulo operator does what I expect.
In Rust, % isn't the same modulo operator. It can return negative numbers. In addition, 10⁹ + 7 is actually very close the the i32 limit. Debugging took a while since LeetCode disables overflow errors, and for the longest time, I couldn't tell why behavior was differing. I had to add modulo operations in several places for the program to work.
Copied!1const MOD: i64 = 1_000_000_007; 2 3impl Solution { 4 pub fn possible_string_count(word: String, k: i32) -> i32 { 5 if k >= word.len() as i32 { 6 return 1; 7 } 8 let mut limit = k - word.len() as i32; 9 let mut prev = word.chars().next().unwrap(); 10 let mut count = 1; 11 let mut counts = Vec::new(); 12 for c in word.chars().skip(1).chain(std::iter::once('\0')) { 13 if c == prev { 14 count += 1; 15 continue; 16 } 17 if count > 1 { 18 counts.push(count); 19 limit += count - 1; 20 } 21 prev = c; 22 count = 1; 23 } 24 let total = counts.iter().fold(1i64, |acc, &count| acc * (count as i64) % MOD) as i32; 25 if limit <= 0 { 26 return total; 27 } 28 let mut ways = vec![1; limit as usize]; 29 counts.iter().for_each(|&count| { 30 for i in 1..limit as usize { 31 ways[i] = (ways[i] + ways[i - 1]) % MOD as i32; 32 } 33 for i in (count..limit).rev() { 34 ways[i as usize] = (ways[i as usize] - ways[(i - count) as usize]) % MOD as i32; 35 } 36 }); 37 (total - ways[limit as usize - 1]).rem_euclid(MOD as i32) 38 } 39}
Not the prettiest code, but it's good enough.
Globally caching the answer probably wasn't the intended solution, but I was feeling lazy. The actual solution probably involves operations on powers of 2.
Copied!1word = "a" 2shift = lambda c: 'a' if c == 'z' else chr(ord(c) + 1) 3while len(word) < 500: 4 word += ''.join(map(shift, word)) 5 6class Solution: 7 def kthCharacter(self, k: int) -> str: 8 return word[k - 1]
Back in my day (last summer) it was one Hard per week. Why's it two now?!
😡
To be fair, this problem was more of a Medium. It was definitely the easiest Hard I've done. I did get punished a little for cheesing yesterday's problem, but I had fun working through the algorithm today.
Today also marked a rare occurrence of everything working first try. I had zero off-by-one errors, even on the local testcases. It definitely helped to walk through an example beforehand.
Copied!1# length of word 2# 1 -> 2 -> 4 -> 8 ... 3# if all 1s 4# abbcbccdbccdcdde 5# 0 -> 2: +1 6# 0 -> 4: +1 7# 0 -> 8: +1 8# powers of 2 -> take number of 1's up to that point 9# 2^0 2^1 2^2 ... 10# [ number of 1's up to that power of 2 ] 11# pow +1 +2 +4 +8 12# inc +0 +1 +0 +1 13# index 9
I considered situations where all operations are 1 (essentially yesterday's problem) and where is a power of 2. From there I had the insight to jump by diminishing powers of 2 up to since the impact of each jump can be calculated.
Copied!1class Solution: 2 def kthCharacter(self, k: int, operations: List[int]) -> str: 3 k -= 1 4 total = 0 5 for op in operations: 6 total += k & 1 and op 7 k >>= 1 8 if not k: 9 return chr(total % 26 + 97)
Just for fun, here's a one-liner.
Copied!1class Solution: 2 def kthCharacter(self, k: int, operations: List[int]) -> str: 3 return chr(sum((k - 1) >> i & op for i, op in enumerate(operations)) % 26 + 97)
And of course, a Rust implementation.
Copied!1impl Solution { 2 pub fn kth_character(k: i64, operations: Vec<i32>) -> char { 3 ((operations.iter().take(64 - (k - 1).leading_zeros() as usize).enumerate().map(|(i, &op)| { 4 (k - 1 >> i) as i32 & op 5 }).sum::<i32>() % 26) as u8 + b'a') as char 6 } 7}
Pretty standard Easy today. Just throw a Counter at it.
Copied!1class Solution: 2 def findLucky(self, arr: List[int]) -> int: 3 return max(map(lambda nf: nf[0] if nf[0] == nf[1] else -1, Counter(arr).items()))
This problem was also pretty easy. I thought a little about a complicated add function that would allow me to keep both lists sorted. With the lists sorted, count could iterate through them in opposite directions and run in linear time. But then I decided to apply the third Law of LeetCode:
- Just throw a
Counterat it.
I'll compile them onto a page eventually.
Copied!1class FindSumPairs: 2 3 def __init__(self, nums1: List[int], nums2: List[int]): 4 self.c1 = Counter(nums1) 5 self.c2 = Counter(nums2) 6 self.nums2 = nums2 7 8 def add(self, index: int, val: int) -> None: 9 self.c2[self.nums2[index]] -= 1 10 self.nums2[index] += val 11 self.c2[self.nums2[index]] = self.c2.get(self.nums2[index], 0) + 1 12 13 def count(self, tot: int) -> int: 14 return sum(c1 * self.c2.get(tot - n1, 0) for n1, c1 in self.c1.items()) 15 16# Your FindSumPairs object will be instantiated and called as such: 17# obj = FindSumPairs(nums1, nums2) 18# obj.add(index,val) 19# param_2 = obj.count(tot)
I think this was a good Medium. Originally, I thought I could just sort the events by start and end times and then take them greedily, but that got shut down by testcase 35. I don't regret rushing though. I struggled to brainstorm testcases on this problem, but testcase 35 had some nice edge cases that allowed me to plan a more structured approach.
My original submission was quite nasty. It had four while loops with five nesting levels.
Copied!1class Solution: 2 def maxEvents(self, events: List[List[int]]) -> int: 3 # events.sort(key=lambda event: event[0]) 4 events.sort() 5 count = 0 6 cand = [] 7 heapify(cand) 8 idx = 0 9 length = len(events) 10 while idx < length: 11 day = events[idx][0] 12 while idx < length and events[idx][0] == day: 13 heappush(cand, (events[idx][1], events[idx][0])) 14 idx += 1 15 while cand and (idx == length or day < events[idx][0]): 16 while cand: 17 end, start = heappop(cand) 18 if start <= day and day <= end: 19 count += 1 20 break 21 day += 1 22 return count
🤮
A little refactoring later, I had this.
Copied!1class Solution: 2 def maxEvents(self, events: List[List[int]]) -> int: 3 events.sort(key=lambda event: event[0]) 4 count = 0 5 cand = [] 6 heapify(cand) 7 day = 1 8 events.append([0, 0]) 9 for event in events: 10 while cand and day != event[0]: 11 end, start = heappop(cand) 12 if start <= day and day <= end: 13 count += 1 14 day += 1 15 heappush(cand, (event[1], event[0])) 16 day = event[0] 17 return count
It pains me to use both sort and a heap on one problem, but I think it was required.
This problem wasn't too bad. I don't think it was necessarily easier than most Hard problems I've done, but things worked out more smoothly than usual. My full submission passed once I got all the local cases working.
My friends looked at the topics list and mentioned dynamic programming, so I formed a rough plan pretty quickly. It felt natural to sort the events and run dynamic programming on the start day. It also felt natural to pass around the k constraint such that each event would (1) move the start day and (2) decrement kk.
Since multiple start_day inputs could be equivalent (it's always optimal to skip to the next actual start day), I set up a sort of "sled" on line 10. Shoutout to the bisect library. I didn't have to write my own binary search. Yay!
Interestingly, passing idx values down to limit the bisect_left search space actually hurt runtime. Go figure.
Of course, I encountered some edge cases:
kkhitting 0 (lines 8-9)idxreachinglength(lines 11-12)- Needing to skip all events on
start_day(lines 22-25)
Anyways, here's the code.
Copied!1class Solution: 2 def maxValue(self, events: List[List[int]], k: int) -> int: 3 events.sort(key=lambda event: event[0]) 4 length = len(events) 5 best = defaultdict(lambda: defaultdict(int)) 6 7 def memo(start_day, kk): 8 if kk == 0: 9 return 0 10 idx = bisect_left(events, [start_day, 0, 0]) 11 if idx == length: 12 return 0 13 start_day = events[idx][0] 14 if start_day in best and kk in best[start_day]: 15 return best[start_day][kk] 16 best_score = 0 17 while idx < length and events[idx][0] == start_day: 18 score = events[idx][2] + memo(events[idx][1] + 1, kk - 1) 19 if score > best_score: 20 best_score = score 21 idx += 1 22 if idx < length: 23 score = memo(start_day + 1, kk) 24 if score > best_score: 25 best_score = score 26 best[start_day][kk] = best_score 27 return best_score 28 29 return memo(events[0][0], k)
My runtime beats around 25%. I considered optimizing or refactoring but probably don't have enough time. My solution uses memoization, not dynamic programming, so it's a bit slower because of all the if checks and the need for dictionaries.
I decided not to use a 2D array (the typical DP setup) since startDay ranged up to 10⁹. Based on submissions I looked at, dynamic programming on the index within events would have been simpler and faster, but whatever.
Nevermind, I found the time. Converting my old code actually wasn't too difficult. I just refactored using the following steps:
- Replace
start_daywithstart_idxand remove thewhileloop since indices are unique. At each point, we either attend or skip. - Replace the dictionary of dictionaries with 2D array. Pre-allocation is faster, and based on the constraints, memory usage is reasonable when using indices.
- Convert
memoto dynamic programming. We guarantee that prerequisite cells are filled, eliminating the need forifstatements and recursive stack frames. - Swap the loop order so
idxcan be reused. Originally, I my outer loop was iterating onk, so I had to runbisect_leftat every cell. Withstart_idxas the outer loop,idxwill match acrosskvalues.
Copied!1class Solution: 2 def maxValue(self, events: List[List[int]], k: int) -> int: 3 events.sort(key=lambda event: event[0]) 4 length = len(events) 5 best = [[0] * (k + 1) for _ in range(length)] 6 best[length - 1][1:] = [events[length - 1][2]] * k 7 8 for start_idx in reversed(range(length - 1)): 9 idx = bisect_left(events, [events[start_idx][1] + 1, 0, 0]) 10 for kk in range(1, k + 1): 11 attend = events[start_idx][2] + (best[idx][kk - 1] if idx < length else 0) 12 skip = best[start_idx + 1][kk] 13 best[start_idx][kk] = attend if attend > skip else skip 14 15 return best[0][k]
Shorter. Faster. What more could I wish for?
A Greedy linear problem. My favorite!
This problem should have been a lesson on the importance of reading. I say "should have" because my haste didn't cost me that much, though it led to some hiccups. To be fair, the problem had a long description, and four input variables is a lot.
First, I misinterpreted the constraint...
Note that the meetings can not be rescheduled to a time outside the event.
...as...
Note that the meetings can not be rescheduled to a time outside [their original time].
...which might have made the problem significantly harder. I gave and reread the prompt soon after though. I also completed missed the constraint that...
The relative order of all the meetings should stay the same and they should remain non-overlapping.
I accidentally inferred these conditions and worked with @Chloe to brainstorm a solution around them. Only later did we consider more efficient strategies such as keeping meetings fixed and moving meetings to fill the gaps. Sometimes I wonder if I'm doing too much LeetCode.
We also considered pushing events in both directions but concluded that shifting all k events to one side would be equivalent.
From there, I only had to worry about off-by-one errors and how to handle the initialization of variables.
Copied!1class Solution: 2 def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int: 3 length = len(startTime) 4 duration = sum(endTime[:k]) - sum(startTime[:k]) 5 startTime.append(eventTime) 6 space = startTime[k] 7 best = space - duration 8 for i in range(k, length): 9 space = startTime[i + 1] - endTime[i - k] 10 duration += endTime[i] - startTime[i] 11 duration -= endTime[i - k] - startTime[i - k] 12 if space - duration > best: 13 best = space - duration 14 return best
I swear, the amount of times I wrote k instead of i.
This problem was just asking for a generator solution, so I wrote one in Rust.
Copied!1impl Solution { 2 pub fn max_free_time(event_time: i32, k: i32, start_time: Vec<i32>, end_time: Vec<i32>) -> i32 { 3 let blocks = start_time 4 .iter() 5 .chain(std::iter::once(&event_time)) 6 .zip(std::iter::once(&0).chain(end_time.iter())) 7 .map(|(a, b)| a - b); 8 let init = blocks.clone().take(k as usize + 1).sum::<i32>(); 9 blocks 10 .clone() 11 .skip(k as usize + 1) 12 .zip(blocks.clone()) 13 .map(|(a, b)| a - b) 14 .fold((init, init), |(duration, max), delta| { 15 (duration + delta, max.max(duration + delta)) 16 }) 17 .1 18 } 19}
Regrettable decision. I love Rust functional programming, but efficient sliding window sums are more of an imperative programming construct.
This problem was decent but not as fun as yesterday's. @Chloe and I worked together again. We decided to test events one by one to see which could create the biggest gap.
I originally forgot to consider that an optimal solution could involve shifting an event into an adjacent gap, but we got there while considering edge cases. (She didn't count adjacent shifts as edge cases, but they felt edgy to me.)
Anyways, this problem seemed annoying to program, so I let her do it.
Copied!1class Solution: 2 def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int: 3 output = 0 4 heap, gaps = [], [] 5 length = len(startTime) 6 7 for i in range(length + 1): 8 if i == 0: # First gap 9 gap = startTime[0] 10 elif i == length: # Last gap 11 gap = eventTime - endTime[-1] 12 else: 13 gap = startTime[i] - endTime[i - 1] 14 heapq.heappush(heap, (-gap, i)) 15 gaps.append(gap) 16 17 largest_gaps = heapq.nsmallest(3, heap) 18 19 for i in range(length): 20 space = endTime[i] - startTime[i] 21 can_move = False 22 23 for (gap, j) in largest_gaps: 24 if j == i or j == i + 1 or space > -gap: 25 continue 26 can_move = True 27 break 28 29 if not can_move: 30 space = 0 31 32 output = max(output, gaps[i] + space + gaps[i + 1]) 33 34 return output
This submission scored 67.05% on runtime and 8.67% on memory, so naturally, I had to refactor it.
Copied!1class Solution: 2 def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int: 3 startTime.append(eventTime) 4 gap_bounds = zip(chain([0], endTime), startTime) 5 largest_gaps = nlargest(3, ((ge - gs, ge) for gs, ge in gap_bounds)) 6 prev_end = 0 7 output = 0 8 for i, (start, end) in enumerate(zip(startTime, endTime)): 9 penalty = end - start 10 for (gap, ge) in largest_gaps: 11 if end != ge - gap and start != ge and penalty <= gap: 12 penalty = 0 13 break 14 score = startTime[i + 1] - prev_end - penalty 15 prev_end = end 16 if score > output: 17 output = score 18 return output
Improving runtime wasn't too bad. I just made two changes:
- Replace
heappushcalls fori >= 3withheappushpopcalls, so the heap stays at or below three elements. Insertions can then run in constant time. - Replace
maxwith a comparison and an assignment. This change actually works on many problems. The Pythonmaxoperator is slow for comparing two numbers since it's overloaded to take several parameter types—lists, iterables, even*args.
These edits got runtime to 98.84% and freed us from the negative heap insertions, but from there, we still had two loops, several if statements, and a boolean flag. Removing them was actually quite difficult.
Recomputing differences instead of storing gaps was probably the biggest breakthrough. It allowed me to replace the heap loop with one call to nlargest. Since nlargest takes an iterator and only ever stores three elements, it stays efficient.
Since startTime and endTime contain distinct elements, largest_gaps can store ge (the end of the gap) instead of i (the loop variable from our original submission).
The gap computation on line 14 isn't lovely, but I'm satisfied with what we have.
I feel like the Hard problems haven't been too bad lately. Just a small step up from Medium problems. I'm not complaining though.
My friends and I figured the solution would involve a heap and simulation. They ditched me for the actual programming, but luckily, implementation went pretty smoothly.
Copied!1class Solution: 2 def mostBooked(self, n: int, meetings: List[List[int]]) -> int: 3 meetings.sort(key=lambda meeting: meeting[0]) 4 rooms = [(0, room) for room in range(n)] 5 uses = [0] * n 6 heapify(rooms) 7 for start, end in meetings: 8 room_start, room = heappop(rooms) 9 if start > room_start: 10 room_end = end 11 else: 12 room_end = room_start + end - start 13 uses[room] += 1 14 heappush(rooms, (room_end, room)) 15 return max(range(len(uses)), key=uses.__getitem__)
Unfortunately, our strategy overlooked an important detail captured by testcase 68.
> meetings = [[18,19],[3,12],[17,19],[2,13],[7,10]]
When multiple rooms are available, our program prioritizes release time over room number, so higher rooms can be erroneously selected. Such a shame. I got excited when the local cases passed first try.
Anyways, during my shower, I brainstormed the idea of creating two heaps, one to store a list of free rooms, and one to store information on room cooldowns.
Copied!1class Solution: 2 def mostBooked(self, n: int, meetings: List[List[int]]) -> int: 3 meetings.sort(key=lambda meeting: meeting[0]) 4 free = list(range(n)) 5 heapify(free) 6 cooldown = [] 7 uses = [0] * n 8 for start, end in meetings: 9 room_start = 0 10 while cooldown and cooldown[0][0] <= start: 11 heappush(free, heappop(cooldown)[1]) 12 if free: 13 room = heappop(free) 14 else: 15 room_start, room = heappop(cooldown) 16 end += room_start - start 17 uses[room] += 1 18 heappush(cooldown, (end, room)) 19 return max(range(len(uses)), key=uses.__getitem__)
Two heaps was a little weird, but I thought it was elegant enough. Finding the index of the largest list element was also quite nice. Credit to Stack Overflow for that one.
Time for two new Laws of LeetCode:
- Go shower. You probably stink.
- Just throw a heap at it.
With regard to the former, my showers can be quite productive. The break really gets ideas flowing.
As for the latter, I know the Laws of LeetCode tend to express irony, but heaps are genuinely pretty cool. They can be there in spite of me liking them.
What happened to doing fun problems?
😡
This problem was on par with Kth Smallest Product of Two Sorted Arrays in terms of pain. Originally, I thought there would be a Math solution analyzing the number players on the left and right of the first and second players, respectively. But after failing several consecutive testcases in the 20s, I realized there were way too many edge cases.
How exciting.
Thus, I gave in and read the topics. Lo and behold, it was Dynamic Progamming.
I decided to operate on counts of players to the left, middle, and right of the first and second players. By symmetry, I constrained l to always be less than (or equal to) r, so the ll loop was easy to set up. The r players give full flexibility.
On the other hand, rmin and rmax brought a ton of edge cases. There were restrictions based on the choice of ll, the locations of the first and second players, and how far the right players extended past the center point, if at all.
And to cause a little more suffering, they included the possibility of an automatically-advancing center player.
Copied!1memo_table = [[[None] * 27 for _ in range(27)] for _ in range(27)] 2 3class Solution: 4 def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]: 5 def memo(l, m, r): 6 if l == r: 7 return [1, 1] 8 if l > r: 9 l, r = r, l 10 if memo_table[l][m][r] is not None: 11 return memo_table[l][m][r] 12 total = l + m + r + 2 13 remaining = (total >> 1) + (total & 1) 14 out = [100, 0] 15 forced = r - (total >> 1) if r - (total >> 1) > 0 else 0 16 for ll in range(l + 1): 17 rmin = l - ll + forced 18 cutoff = remaining - forced 19 rmax = rmin + (r if r < cutoff else cutoff) - (l + 1) 20 if l + 1 + m + 1 <= total >> 1: 21 rmax -= 1 22 # print(l, m, r, ll, rmin, rmax, remaining) 23 for rr in range(rmin, rmax + 1): 24 mm = remaining - ll - rr - 2 25 earliest, latest = memo(ll, mm, rr) 26 if earliest + 1 < out[0]: 27 out[0] = earliest + 1 28 if latest + 1 > out[1]: 29 out[1] = latest + 1 30 # print(l, m, r, out) 31 memo_table[l][m][r] = out 32 return out 33 left = firstPlayer - 1 34 right = n - secondPlayer 35 return memo(left, n - left - right - 2, right)
This is the first time I've waited until the morning after to finish the daily. Living on the edge out here. Unfortunately, that means no time to refactor. I repeated total >> 1 on several lines, and a lot of numbers inside the ll loop are independent of ll, but I can't be bothered to fix it.
This Medium was more of an Easy. Sort, sort, iterate, win. I spent longer waiting for my internet to load than solving the problem.
Copied!1class Solution: 2 def matchPlayersAndTrainers(self, players: List[int], trainers: List[int]) -> int: 3 players.sort() 4 trainers.sort() 5 length = len(players) 6 idx = 0 7 for trainer in trainers: 8 if players[idx] <= trainer: 9 idx += 1 10 if idx == length: 11 break 12 return idx
Interestingly, they added this note at the end. Don't think I've ever seen it before.
Note: This question is the same as 445: Assign Cookies.
Definitely the easiest problem so far. Bit operations always feel so cool.
Copied!1class Solution: 2 def getDecimalValue(self, head: Optional[ListNode]) -> int: 3 out = head.val 4 while head.next: 5 head = head.next 6 out = (out << 1) + head.val 7 return out
Well, yesterday's problem was the easiest for a grand total of one day.
Copied!1class Solution: 2 def isValid(self, word: str) -> bool: 3 return len(word) >= 3 and word.isalnum() and any(v in word for v in 'aeiouAEIOU') and any(c in word for c in 'bcdfghjklmnpqrstvwxyzBCDFGHJKLMNPQRSTVWXYZ')
I followed the instructions. Guess I got to practice typing the alphabet. Yippee!
These past several posts have been quite short. Post length tends to mirror problem difficulty. But do not fret, I anticipate a Hard soon.
Harder than yesterday, but still on the easier end of Medium problems. Just a little parity tracking.
Copied!1class Solution: 2 def maximumLength(self, nums: List[int]) -> int: 3 # every other has same parity 4 # EE 5 # EO 6 # OE 7 # OO 8 count = [0] * 4 9 parity = [0, 1] 10 for num in nums: 11 if num & 1: 12 count[0] += 1 13 else: 14 count[1] += 1 15 if num & 1 == parity[0]: 16 count[2] += 1 17 parity[0] = not parity[0] 18 if num & 1 == parity[1]: 19 count[3] += 1 20 parity[1] = not parity[1] 21 return max(count)
My original submission was pretty slow. I'm not positive what caused it (maybe the lists), but I did some optimization and got runtime to 95.35%. Searching for optimizations was kinda fun. In order of implementation:
- Switching to a single parity counter. The two subsequences with alternating parity share most entries, but the subsequence starting on the parity of the first number always wins.
- Only counting odd numbers. The number of even numbers can then be calculated from total length.
- Using two counter variables instead of a list.
Copied!1class Solution: 2 def maximumLength(self, nums: List[int]) -> int: 3 length = len(nums) 4 odd = swap = 0 5 parity = nums[0] & 1 6 for num in nums: 7 if num & 1: 8 odd += 1 9 if num & 1 == parity: 10 swap += 1 11 parity = not parity 12 return max(odd, length - odd, swap)
Was planning to ship UI improvements today, but I got lazy.
Finally, a real Medium. I think I struggled the right amount on this problem, both on formulating a plan and on implementation.
At first, I had several nebulous ideas about dynamic programming and storing sequences. A big breakthrough was realizing that the problem is equivalent to searching for a subsequence where every other number is congruent mod k. It took a while to convert that to something concrete though.
Here's my first serious submission:
Copied!1class Solution: 2 def maximumLength(self, nums: List[int], k: int) -> int: 3 # subsequence where every other number is congruent mod k 4 # 5 # lengths[i][j] 6 lengths = [[0] * k for _ in range(k)] 7 active = [[True] * k for _ in range(k)] 8 out = 0 9 for num in nums: 10 num %= k 11 for i, a in enumerate(active[num]): 12 if a: 13 active[num][i] = False 14 active[i][num] = True 15 if i > num: 16 i, num = num, i 17 lengths[num][i] += 1 18 return max(map(max, lengths))
With implementation, I mainly struggled with the fact that certain i-num sets are equivalent and should share a length counter. Unfortunately, my initial method for correcting this was to swap i and num when i > num.
For individual loop iterations, this works fine, but num gets messed up. With print statements, I quickly pinpointed the erroneous active settings, but working forward through my code instead of backward from the debug messages cost me a lot of time.
Copied!1class Solution: 2 def maximumLength(self, nums: List[int], k: int) -> int: 3 # subsequence where every other number is congruent mod k 4 lengths = [[0] * c for c in range(1, k + 1)] 5 active = [[True] * k for _ in range(k)] 6 out = 0 7 for num in nums: 8 num %= k 9 for i, a in enumerate(active[num]): 10 if a: 11 active[num][i] = False 12 active[i][num] = True 13 if i > num: 14 lengths[i][num] += 1 15 else: 16 lengths[num][i] += 1 17 return max(map(max, lengths))
After reading some top submissions, I refactored my code to (well... stole) this solution:
Copied!1class Solution: 2 def maximumLength(self, nums: List[int], k: int) -> int: 3 lengths = [[0] * k for _ in range(1, k + 1)] 4 for num in nums: 5 num %= k 6 for i in range(k): 7 lengths[i][num] = lengths[num][i] + 1 8 return max(map(max, lengths))
Very elegant. The active array is unnecessary because worst case, we just overwrite with the same value.
There's the Hard I've been anticipating. This was definitely my favorite Hard so far and possibly my favorite of the problems I've reviewed. The algorithm was neither immediately evident nor painfully difficult to find and did not rely on overused techniques like Binary Search or Dynamic Programming.
@Chloe and I just started brainstorming and eventually discussed using a whiteboard. She had the idea to look at different cutoff points within the middle elements, and I had the idea to generate optimal sums in both directions.
The solution was linear. The solution was Greedy. The elements of a good problem.
Copied!1class Solution: 2 def minimumDifference(self, nums: List[int]) -> int: 3 n = len(nums) // 3 4 left = [-num for num in nums[:n]] 5 l = -sum(left) 6 heapify(left) 7 right = nums[2*n:].copy() 8 r = sum(right) 9 heapify(right) 10 best = [l] * (n + 1) 11 for i in range(n, 2*n): 12 l += nums[i] + heappushpop(left, -nums[i]) 13 best[i + 1 - n] = l 14 best[n] -= r 15 for i in reversed(range(n, 2*n)): 16 r += nums[i] - heappushpop(right, nums[i]) 17 best[i - n] -= r 18 return min(best)
Implementation also had relatively few off-by-one errors.
Pretty average Medium problem, maybe on the easier side. At first, the problem seemed very painful (strings, ew), but most pain was ultimately mitigated by lovely Python abstractions.
Copied!1class Solution: 2 def removeSubfolders(self, folder: List[str]) -> List[str]: 3 folder.sort() 4 top = '.' 5 out = [] 6 for f in folder: 7 if not f.startswith(top): 8 out.append(f) 9 top = f + '/' 10 return out
Initially, I was failing testcase 3. I assumed that my algorithm could not deal with multi-character folders and went into a mini crisis considering runtime- and memory-efficient ways to split strings on delimiters.
Then I realized I forgot to add a '/' on line 9. Big crisis averted by mini crisis.
Just when I thought I was getting the hang of it...
The last several problems were pretty easy. Conceptually, this Hard was the hardest problem I've covered. The other problems I've complained about were only difficult because of tedious edge cases during implementation.
I guess I have the most experience with Array problems. This problem used a Trie. Trees are scary. I was very tempted to use an array anyways.
@Chloe and I did some discussion but didn't make a lot of progress. We mainly thought about the best order to traverse the tree and various ways to store what folder structures have been seen.
We eventually folded and looked at the topics and hints. At the time, they didn't seem very useful, but in hindsight, they essentially summed up the solution.
I guess we mainly struggled because we were searching for an efficient solution. Perhaps no such solution exists. My solution just
- Built a Trie
- Made and cached a hash for every subtree
- Noted duplicate hashes and removed corresponding nodes
Long story short, build a Trie and immediately convert it to a string Array because arrays are easier to work with.
My hash function felt extremely inefficient (the hash of a node is essentially the hashes of its children joined with tree depth as a delimiter). The testcases were probably pretty short since I got 65.17% runtime with the ugliest mess of data structures I've ever written.
I had a Trie to store the folder structure. I also had a Hash Table to convert from Trie nodes to actual paths, a Hash Table to convert from Trie nodes to hashes, two sets to identify duplicate hashes, and a list to build the output.
Anyways, here's my solution in all its glory:
Copied!1class Solution: 2 def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]: 3 root = dict() 4 pathdict = dict() 5 # build trie 6 for path in paths: 7 parent = root 8 for seg in path: 9 parent = parent.setdefault(seg, {}) 10 pathdict[id(parent)] = path 11 12 cache = {} 13 # hash everything (dynamic programming) 14 # function that takes parent (input dict) 15 # sort keys 16 # get height and hash of each child 17 # hash = child hashes separated by max height + 1 as delimiter 18 def hash(parent): 19 height = 1 20 hashes = [] 21 for key in sorted(parent.keys()): 22 c_height, c_hash = hash(parent[key]) 23 if c_height >= height: 24 height = c_height + 1 25 hashes.append(key + ':' + c_hash) 26 cache[id(parent)] = str(height) + str(height).join(hashes) 27 return height, cache[id(parent)] 28 hash(root) 29 30 # print(cache) 31 32 # note duplicate hashes 33 seen = set() 34 dupes = {h for h in cache.values() if len(h) > 1 and h in seen or seen.add(h)} 35 # print(dupes) 36 37 # re-traverse trie, check if own hash is unique and 38 # hashes of any children are unique 39 # if removing, early out, prevent leaves from being added 40 # inspect = id(root['a']['b']) 41 out = [] 42 def check(parent): 43 # if id(parent) == inspect: 44 # print(parent.values()) 45 # print(any(cache[id(child)] not in dupes for child in parent.values())) 46 # if parent != root: 47 # out.append(pathdict[id(parent)]) 48 # if cache[id(parent)] not in dupes and any(cache[id(child)] not in dupes for child in parent.values()): 49 # for child in parent.values(): 50 # check(child) 51 if cache[id(parent)] not in dupes: 52 if parent != root: 53 out.append(pathdict[id(parent)]) 54 for child in parent.values(): 55 check(child) 56 check(root) 57 # print(out) 58 return out 59 60 # write height at start of hash? 61 # custom data structure? 62 # better hash function? use tuples and builtin hash? 63 64 # hashmap - node to representative node 65 # or hash function should use things I can point to 66 # instead of immutable strings
By the way, Trie's are much less intuitive to than normal trees. The Trie I built (well, stole from Reddit 😉) was just a bunch of nested dictionaries. To traverse the children of a node, you run .values().
Consider the following example:
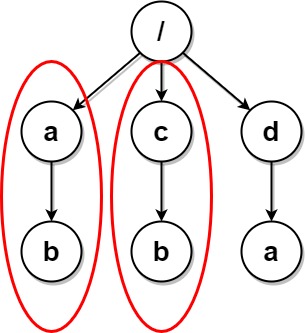
Running root.values() brings you straight to the bottom level. The middle level is stored as dictionary keys. This plagued me on the check function. I still don't fully understand what was happening.
My first submission passed exactly 107/108 testcases. I managed to make a hash function that was good but not quite good enough. My solution? Just tack on an extra delimiter.
Anyways, if LeetCode starts a daily Tree arc, I might cry.
Well, after yesterday's train wreck, this Easy was in fact easy.
Copied!1class Solution: 2 def makeFancyString(self, s: str) -> str: 3 count = None 4 prev = None 5 out = '' 6 for c in s: 7 if c == prev: 8 if count == 2: 9 continue 10 count += 1 11 else: 12 prev = c 13 count = 1 14 out += c 15 return out
I wonder if line count can be reduced (through logical improvements, not cursed Python syntax).
Anyways, what does the term "fancy" have to do with a string containing no triple characters??? I don't see the connection.
Good Medium. Linear solution. Gonna go play Minecraft. Bye!
Copied!1class Solution: 2 def maximumUniqueSubarray(self, nums: List[int]) -> int: 3 length = len(nums) 4 index = [-1] * (10 ** 4 + 1) 5 l = 0 6 score = 0 7 best = 0 8 for i, num in enumerate(nums): 9 while l <= index[num]: 10 score -= nums[l] 11 index[nums[l]] = -1 12 l += 1 13 index[num] = i 14 score += num 15 if score > best: 16 best = score 17 return best
My first instance of having completed the daily already!
Based on the submission history, this problem was the daily on July 12 last year. I just barely remember doing it with @Chloe.
I guess today I get to see how readable my code was.
Copied!1class Solution: 2 def maximumGain(self, s: str, x: int, y: int) -> int: 3 if x > y: 4 c1, c2, p1, p2 = 'a', 'b', x, y 5 else: 6 c1, c2, p1, p2 = 'b', 'a', y, x 7 points, ct1, ct2 = 0, 0, 0 8 for c in s: 9 if c == c1: 10 ct1 += 1 11 elif c == c2: 12 if ct1: 13 ct1 -= 1 14 points += p1 15 else: 16 ct2 += 1 17 else: 18 points += min(ct1, ct2) * p2 19 ct1, ct2 = 0, 0 20 points += min(ct1, ct2) * p2 21 return points
Conclusion: semi-readable. I definitely remember the problem now. It's a pretty cool Greedy algorithm. Smushing substrings together is fun.
The submission scored 98.06% with 135 ms runtime. Replacing line 18 with an if statement brought it to 100.00% with 101 ms runtime. The difference that makes is crazy. It would be a Law of LeetCode if it weren't Python-specific.
Maybe someday I'll need the Laws of Python (LeetCode Edition).
A hard tree problem. Yikes.
In terms of pain, this problem wasn't the worse I've encountered, but I think it would be better as a Medium where only one edge can be cut. Such a problem would still require cleverness but avoid the pain of nested iteration.
To be fair, though, I had a pretty crappy solution.
Since the input edges were undirected, I started with an adjacency matrix and immediately ran a depth-first search produce a (directed) tree structure. The depth-first search also computed XOR values for each subtree.
This part wasn't that cursed (except the method for determining a root node), but in the next part, I used nested depth-first searches to select pairs of edges. This decision felt wrong, and I spent a while trying to avoid it by iterating through edges. Nevertheless, I couldn't think of a fast way to store whether each edge is in the subtree of another.
Long story short, get ready to witness the messiest code I've written. Arguably much worse than last Sunday's spaghetti slop.
Copied!1class Solution: 2 def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int: 3 # build tree 4 length = len(nums) 5 children = [set() for _ in range(length)] 6 for v1, v2 in edges: 7 children[v1].add(v2) 8 children[v2].add(v1) 9 root = next(i for i in range(length) if len(children[i]) == 1) 10 11 # precompute XOR values 12 # make edges directional 13 # TODO: initialize as copy and run xors directly? 14 values = [None] * length 15 def compute(node): 16 val = nums[node] 17 for n in children[node]: 18 children[n].remove(node) 19 val ^= compute(n) 20 values[node] = val 21 return val 22 root_val = compute(root) 23 # print(children) 24 # print(values) 25 26 target = None 27 sv = None 28 rv = None 29 best = float('inf') 30 def dfs_inner(node, state): 31 # print(node, state, nums) 32 nonlocal best 33 score = best 34 if state == 1: 35 # print(rv, sv ^ values[node], values[node]) 36 score = max(rv, sv ^ values[node], values[node]) - min(rv, sv ^ values[node], values[node]) 37 elif state == 2: 38 # print(rv ^ values[node], sv, values[node]) 39 score = max(rv ^ values[node], sv, values[node]) - min(rv ^ values[node], sv, values[node]) 40 if score < best: 41 best = score 42 if node == target: 43 state = 1 44 for child in children[node]: 45 state = dfs_inner(child, state) 46 if node == target: 47 state = 2 48 return state 49 50 # dfs over first edge removal 51 # keep track of two sets: route set and other set 52 # iterate through every node 53 # if in route set, skip 54 # if in subtree, take out of subtree 55 # otherwise, take out of root 56 def dfs_outer(node): 57 nonlocal target, sv, rv 58 for child in children[node]: 59 target = child 60 sv = values[child] 61 rv = root_val ^ sv 62 dfs_inner(root, 0) 63 for child in children[node]: 64 dfs_outer(child) 65 dfs_outer(root) 66 return best
The runtime distribution was quite goofy. Instead of the normal shape, it was a horizontal distribution ranging from 1139 ms to 4720 ms.
Anyways, I looked at some top submissions and noticed that they track in and out times for each node during the initial depth-first search. Membership for any subtree-node combination can then be checked in constant time.
Those solutions were much cleaner, but ultimately, the problem didn't seem to have any particularly concise solutinons.
This problem seemed extremely easy at first. My initial submission was:
Copied!1class Solution: 2 def maxSum(self, nums: List[int]) -> int: 3 return sum(set(nums))
Though more difficult than I first imagined (I took three submissions), it was still the easiest or second easiest problem I have covered.
Copied!1class Solution: 2 def maxSum(self, nums: List[int]) -> int: 3 return sum(filter(lambda n: n > 0, set(nums))) or max(nums)
They're really going rapid fire with these Hard problems.
Initially, I misread "subarray" as "subsequence" and was considering a much harder problem.
After a little while, I looked at the topics and got spooked.
Segment Tree
Yikes. As a bit of backstory, a segment tree problem last summer kept me up until 7 AM and was the closest I got to losing my streak.
So anyways, this problem was hard, and after reading the topics, I had concerns about my streak. Thus, I was a little more liberal with my use of hints and ultimately used two of five.
To be fair, I didn't catch on to the whole "subarray" thing until I had read and fully understood the second hint (which explained how to calculate the total number of subarrays). Needless to say, I was rather confused when the equation lacked any powers of two.
The hints were definitely good hints. They clued me in the right direction but left room for thinking. For example, the first hint mentioned an array that might be useful but glossed over the strategy for efficiently generating it.
I wish I had caught onto the whole "subarray" thing sooner though. I wonder if I could've done the problem without using any hints.
Copied!1class Solution: 2 def maxSubarrays(self, n: int, conflictingPairs: List[List[int]]) -> int: 3 first = [n + 1] * (n + 1) 4 second = [n + 1] * (n + 1) 5 first[0] = 0 6 7 for a, b in conflictingPairs: 8 if a > b: 9 a, b = b, a 10 if b <= first[a]: 11 second[a] = first[a] 12 first[a] = b 13 elif b <= second[a]: 14 second[a] = b 15 16 stop = first.copy() 17 18 for i in reversed(range(n)): 19 if stop[i] > stop[i + 1]: 20 stop[i] = stop[i + 1] 21 22 base = sum(stop) - n * (n + 1) // 2 23 best = base 24 25 for i in range(1, n): 26 score = base 27 old = stop[i] 28 new = second[i] if second[i] < stop[i + 1] else stop[i + 1] 29 while new > old and i > 0: 30 score += new - old 31 i -= 1 32 old = stop[i] 33 new = first[i] if first[i] < new else new 34 if score > best: 35 best = score 36 37 return best
I'm not sure if this is the best solution, but the code felt reasonably concise. I wasn't expecting it to pass though, let alone score 99.10% on runtime, since it didn't use a segment tree.
I was so prepared to lock in all night that I microwaved some ramen, but my submission succeeded right as I was delivering the ramen to the table. I ended up playing some Dance Dance Revolution to pass the time.
A nice, refreshing Easy after all those hard problems. A couple annoying edge cases but nothing too serious. Maybe there's a nicer solution, but at least compared to the provided samples, I think I did pretty well.
Copied!1class Solution: 2 def countHillValley(self, nums: List[int]) -> int: 3 direction = 0 4 count = 0 5 for a, b in zip(nums, nums[1:]): 6 if direction == 0 and b != a: 7 direction = 1 if b > a else -1 8 if direction * (b - a) < 0: 9 direction = -direction 10 count += 1 11 return count
Not the most interesting Medium but not the worst. I tend to dislike problems that require generation of combinations, permutations, or subsets. Based on the constraint that 1 <= nums.length <= 16, I figured the solution would be somewhat brute force.
Copied!1class Solution: 2 def countMaxOrSubsets(self, nums: List[int]) -> int: 3 maximum = reduce(operator.or_, nums) 4 count = 1 5 for k in range(1, len(nums)): 6 for combination in combinations(nums, k): 7 if reduce(operator.or_, combination) == maximum: 8 count += 1 9 return count
My initial submission was fully brute force and also quite slow. I decided to refactor for runtime by lumping equivalent numbers together.
Copied!1class Solution: 2 def countMaxOrSubsets(self, nums: List[int]) -> int: 3 maximum = reduce(operator.or_, nums) 4 counts = defaultdict(int) 5 counts[0] = 1 6 for num in nums: 7 for n, c in list(counts.items()): 8 counts[n | num] += c 9 return counts[maximum]
This problem was decent, though my solution wasn't great. My initial submission was extremely ugly and scored 29.92% on runtime.
Copied!1class Solution: 2 def smallestSubarrays(self, nums: List[int]) -> List[int]: 3 counts = [0] * 32 4 size = 0 5 out = [0] * len(nums) 6 for l in reversed(range(len(nums))): 7 size += 1 8 push = nums[l] 9 idx = 0 10 while push: 11 if push & 1: 12 counts[idx] += 1 13 idx += 1 14 push >>= 1 15 success = True 16 while success and size > 1: 17 idx = 0 18 pop = nums[l + size - 1] 19 while pop: 20 if pop & 1: 21 counts[idx] -= 1 22 if counts[idx] == 0: 23 success = False 24 idx += 1 25 pop >>= 1 26 if success: 27 size -= 1 28 else: 29 idx = 0 30 push = nums[l + size - 1] 31 while push: 32 if push & 1: 33 counts[idx] += 1 34 idx += 1 35 push >>= 1 36 out[l] = size 37 return out
I was honestly a little surprised it did so poorly, but I suppose it had three nested loops and five layers of nesting.
I refactored a little and got runtime up to 85.04%, but the code is still pretty ugly, and its runtime is triple that of the top submissions.
Copied!1class Solution: 2 def smallestSubarrays(self, nums: List[int]) -> List[int]: 3 counts = [0] * 32 4 out = [0] * len(nums) 5 size = 0 6 popidx = 0 7 for l in reversed(range(len(nums))): 8 size += 1 9 push = nums[l] 10 idx = 0 11 while push: 12 if push & 1: 13 counts[idx] += 1 14 idx += 1 15 push >>= 1 16 success = True 17 while success and size > 1: 18 pop = nums[l + size - 1] 19 while pop: 20 if pop & 1: 21 if counts[popidx] == 1: 22 nums[l + size - 1] = pop 23 success = False 24 break 25 counts[popidx] -= 1 26 popidx += 1 27 pop >>= 1 28 if success: 29 size -= 1 30 popidx = 0 31 out[l] = size 32 return out
Unfortunately, I have a poster due Friday, so I don't really have time to fix it.
I guess they made this problem Medium because it's the AND version of yesterday's problem, but this problem was more of an Easy, both conceptually and during implementation.
Copied!1class Solution: 2 def longestSubarray(self, nums: List[int]) -> int: 3 maximum = max(nums) 4 count = 0 5 best = 0 6 for num in nums: 7 if num == maximum: 8 count += 1 9 if count > best: 10 best = count 11 else: 12 count = 0 13 return best
Lots of bitwise operator problems lately. I'm all for it. Although today's problem didn't actually require any bitwise operators.
Top submissions have a cool use of the groupby function.
Copied!1class Solution: 2 def longestSubarray(self, nums: List[int]) -> int: 3 maximum = max(nums) 4 return max(len(list(it)) for n, it in groupby(nums) if n == maximum)
Damn. This problem took me a while. It's the kind of problem that seems like it should have a nice, linear solution, but it ended up being sort of brute force.
Copied!1class Solution: 2 def subarrayBitwiseORs(self, arr: List[int]) -> int: 3 prev = [] 4 out = set() 5 for cumulative in arr: 6 curr = [cumulative] 7 out.add(cumulative) 8 for p in prev: 9 if cumulative | p != cumulative: 10 cumulative |= p 11 curr.append(cumulative) 12 out.add(cumulative) 13 prev = curr 14 return len(out)
The whole out = set() part felt bad in addition to the fact that, worst case, my solution would have a time complexity of where is the length of arr. Maybe even if the size of out doubles each iteration.
Anyways, turns out instead of all that thinking, I could have just spammed sets.
Copied!1class Solution: 2 def subarrayBitwiseORs(self, arr: List[int]) -> int: 3 prev = set() 4 out = set() 5 for num in arr: 6 curr = {num} 7 for p in prev: 8 curr.add(p | num) 9 out.update(curr) 10 prev = curr 11 return len(out)
50 days in a row. Hooray!
Anyways, today's problem was particularly easy because I had already done it. I did problems 1-150 last summer. This was problem 118.
Copied!1pt = [[1], [1, 1]] 2for _ in range(2, 30): 3 prev = 0 4 newrow = [] 5 for num in pt[-1]: 6 newrow.append(prev + num) 7 prev = num 8 newrow.append(1) 9 pt.append(newrow) 10 11class Solution: 12 def generate(self, numRows: int) -> List[List[int]]: 13 return pt[:numRows]
Based on constraints, they're only asking for the first 30 rows, so I just generate them and return what's requested. Caching!
I wonder if they expect people to store global variables or if this is a cheesy strategy. I guess I could store things in the class instead, so surely it's fine, right?
This post will be the last for now. Writing has been enjoyable, but this commitment added to the daily LeetCode has cost me a little too much sleep.
I'll report back when I finally ditch the streak.
Summer is over. I'm free!
Normally, the streak would die, but @Chloe has volunteered to keep it alive.
Goodbye for now.